一、引入
最近在刷题的时候,遇到了一些前缀和结合子数组的题目,这些题目,有一个共同的特性,就是说,刚开始都能够想利用前缀和进行优化,然后再结合子序列的左右端点进行枚举,最后确定哪一个区间或者哪一些是能够满足我们的题目要求,但是有一个问题就是,我们在枚举区间的两个端点的时间复杂度是$O(n^2)$的,所以一旦题目数据给的特别大的时候,就会过不了,这个时候就需要利用题目的相关性质结合哈希表解题,把时间复杂度降到$O(n)$以下,就可以过了,这里整理了相关类似的题目,此专题也会持续的更新….
二、题目汇总
①力扣1124.表现良好的最长时间段
原题(来源于leetcode)
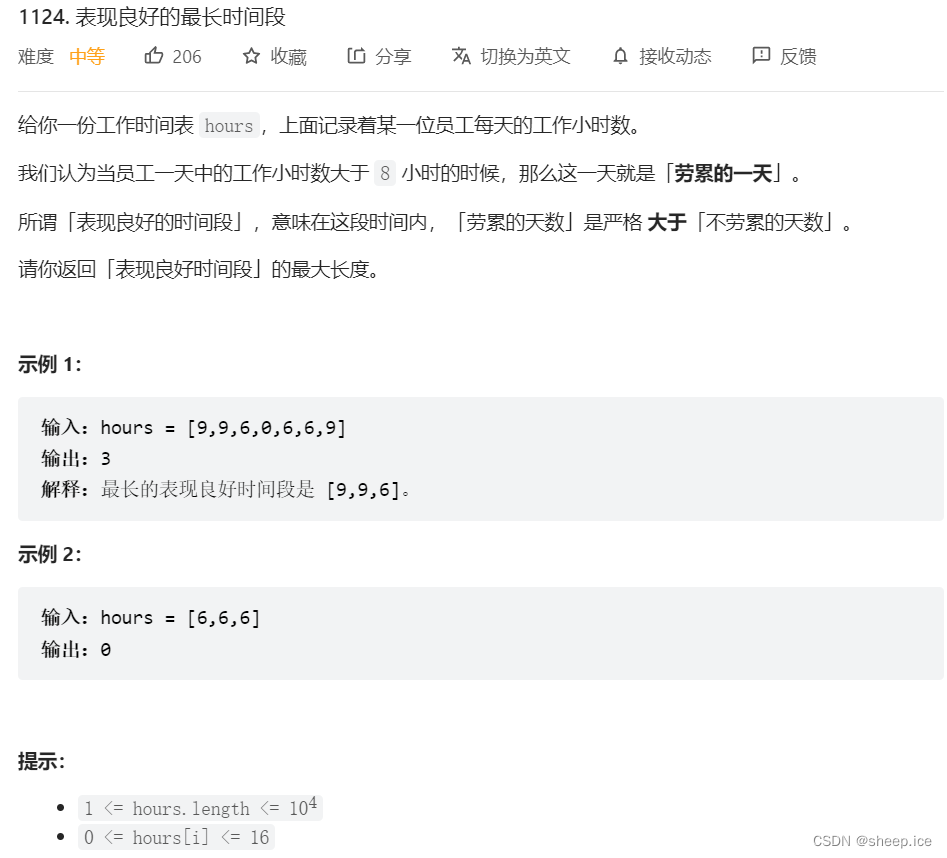
暴力分析
①第一种暴力的想法,就是枚举左右端点,再通过一层循环枚举每一个左右端点形成的区间的表现良好和不良好的时间段的个数,那么一旦符合良好的个数大于我们的不良好的个数,就可以更新我们的答案了,时间复杂度为O(n^3),肯定是过不了的。
②显然我们利用前缀和可以优化一层找良好和不良好时间段的个数,记良好的为1,不良好的为-1,那么一段区间的区间和大于0就说明良好严格大于不良好,那么最终的时间复杂度为$O(n^2)$的,如果n比较小,那么这个方式是可以过的。
优化分析
由于暴力过不去,那么此时我们想的问题应该是,如何不直接两层循环枚举左右端点就可以求出我们的最终结果呢?
提示1
其实这个地方可以说利用了贪心的一个思想,因为题目很明确的说了,求的是最大的子区间长度,那么我们其实不妨,枚举的时候从右往左枚举,对于一个左端点,一旦右端点从最右往左到某一个位置恰好满足题意的话,那么我们就可以不用继续让右端点往左了,因为已经找到一个可能为答案的备选最大值。
提示2
整个问题变成,如何找一段区间长度和大于0,且这个区间的长度是求最大值。我们只需要记录可能成为左端点的下标,并且满足一旦某个点的前缀和成为了我们左端点的备选点后,在他右边所有和他等值的点都不会成为我们的左端点备选点。
提示3
备选点从左到右一定是严格单调下降的,在实现遍历的时候便是利用单调栈的思想。
提示4
这里有一篇相关题解,里面有比较详细的说明。
完整AC代码
class Solution {
public:
int longestWPI(vector<int>& hours) {
int n = hours.size();
vector<int> pre(n + 1, 0);
for(int i = 1; i <= n; i ++ ) {
auto now = hours[i - 1];
if(now > 8) pre[i] = 1;
else pre[i] = -1;
pre[i] += pre[i - 1];
}
stack<int> stk;
int ans = 0;
for(int i = 0; i <= n; i ++ ) {
if(stk.empty() || pre[stk.top()] > pre[i]) stk.push(i);
}
for(int i = n; i >= 0; i -- ) {
if(stk.empty()) break;
if(!stk.empty() && i <= stk.top()) stk.pop();
while(!stk.empty() && pre[i] > pre[stk.top()]) {
ans = max(ans, i - stk.top());
stk.pop();
}
}
return ans;
}
};②力扣525.连续数组
原题(来源于leetcode)

暴力分析
同上一题的分析,可以利用最暴力和一个前缀和优化的方法,时间复杂度分别为$O(n^3)和O(n^2)$。
优化分析
提示1
把所有的0变成-1,利用前缀和,只需要求哪一些区间的区间和为0就好。
提示2
利用哈希表记录第一次出现前缀和为x的下标位置。
提示3
一旦遍历的时候遇到前缀和为x,那么如果前面也出现过前缀和为x的下标,直接利用两个下标差更新答案就好。
完整AC代码
class Solution {
public:
int findMaxLength(vector<int>& nums) {
int n = nums.size();
vector<int> pre(n + 1, 0);
for(int i = 1; i <= n; i ++ ) {
auto now = nums[i - 1];
if(now == 0) pre[i] = -1;
else pre[i] = 1;
pre[i] += pre[i - 1];
}
map<int, int> mp;
mp[0] = 0;
int ans = 0;
for(int i = 1; i <= n; i ++ ) {
auto t = pre[i];
if(mp.count(t)) {
ans = max(ans, i - mp[t]);
}
else {
mp[t] = i;
}
}
return ans;
}
};③力扣560.和为K的子数组
原题(来源于leetcode)

暴力分析
同第一题的分析,可以利用最暴力和一个前缀和优化的方法,时间复杂度分别为$O(n^3)和O(n^2)$。
优化分析
提示1
利用前缀和快速计算区间长度。
提示2
利用哈希表,记录在遍历过的前缀和出现的次数。
完整AC代码
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int n = nums.size();
vector<int> pre(n + 1, 0);
for(int i = 1; i <= n; i ++ ) {
pre[i] = nums[i - 1];
pre[i] += pre[i - 1];
}
map<int, int> mp;
mp[0] = 1;
int cnt = 0;
for(int i = 1; i <= n; i ++ ) {
auto now = pre[i], last = pre[i] - k;
cnt += mp[last];
mp[now] ++ ;
}
return cnt;
}
};④力扣1371.每个元音包含偶数次的最长字符串长度
原题(来源于leetcode)

暴力分析
同前
优化分析
提示1
把元音的使用情况,进行二进制压缩。
提示2
出现检验奇偶个数,利用异或求解。且奇数-奇数为偶数,偶数-偶数为偶数。
完整AC代码
class Solution {
public:
int findTheLongestSubstring(string s) {
int ans = 0, n = s.size();
vector<int> mp(1 << 5, -2);
mp[0] = -1;
int state = 0;
for(int i = 0; i < n; i ++ ) {
auto t = s[i];
if(t == 'a') {
state ^= (1 << 0);
}
else if(t == 'e') {
state ^= (1 << 1);
}
else if(t == 'i') {
state ^= (1 << 2);
}
else if(t == 'o') {
state ^= (1 << 3);
}
else if(t == 'u') {
state ^= (1 << 4);
}
if(mp[state] != -2) {
ans = max(ans, i - mp[state]);
}
else {
mp[state] = i;
}
}
return ans;
}
};


