图论之spfa

一、前言

对于之前有写到的Dijkstra算法，我们发现他只能用来计算边的权值为正的情况，这其实也就是为什么我们需要开一个st数组，对于一个已经被更新过的点来说，他一旦用于更新其他点的时候，我们就不需要再考虑再利用这个点再次更新其他的点。

但是呢，如果点之间的边是负值的时候，就必须去遍历一下所有的边，因为存在负值的时候，负数加正数是会把距离缩短的，所以呢就可以利用遍历所有边的办法去更新点到原点的距离。这就需要用到后续要说的spfa算法，那么在讲这个算法之前，需要了解bellman-ford算法，会先利用这个算法进行一个引入。

本章题大多来源于ACwing,欢迎大家来这个平台一起学习算法！！

二、题目汇总

①bellman-ford(ACwing.853)

相关分析

时间复杂度： $O(mn)$

适用场景： 这个算法可以看到，时间复杂度比较高，所以mn的值要落在$1e7-1e8$之间才能满足不超时，另外，由于这个算法，是从原点出发，外层循环多少次，内层就需要更新多少次边。这个实际含义就是，外层循环多少次，就代表：从原点出发了多少条边，所以能够计算，走多少条边到终点的一个最短距离，注意这个最短距离并不一定是整个图看上去的最短，而是满足了走k条边的最短！

思路： 如果题目规定走k条边，那么按照上述分析，外层循环k次代表走k条边的更新情况，内部循环，更新每一条边，一旦能够更新就更新，不能更新的话，距离保证不变。这里注意由于内层循环更新的是所有的边，所以是有可能发生应该只再原本的基础上衍生1条边，但是衍生出去了2条边。所以需要一个回溯的数组，保存一下上一次更新好的dist数组。而这个串联反应可以举个例子，如下：

假设这个图，如果我们的k只给1的话，那么从1->3的距离最短应该为3，而不是1+1=2。假设我们在更新的时候，还是像之前dijkstra的更新方式，利用dist数组更新的话，那么在仅有的一次循环里面，1->2这条边的距离首先会被更新为1，那么在2->3这条边就会按照dist[2] = 1的这个数组更新dist[3],让dist[3]变成2，那么就和我们最终得到的答案3就是不同的。

完整AC代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 505, M = 10050;
//因为要遍历所有边，所以结构体存图
struct Edge {
    int a, b, c;
}edges[M];
int dist[N], n, m, k;
//设置一个回溯的数组
int backup[N];

void bellman_ford() {
    dist[1] = 0;
    
    for(int i = 1; i <= k; i ++ ) {
        //先进行一个备份操作
        memcpy(backup, dist, sizeof dist);
        
        for(int i = 1; i <= m; i ++ ) {
            auto t = edges[i];
            //就是这个地方，如果写成
            //dist[t.b] > dist[t.a] + t.c的话
            //就会有可能出现串联反应
            if(dist[t.b] > backup[t.a] + t.c) {
                dist[t.b] = backup[t.a] + t.c;
            }
        }
    }
}

int main() {
    cin >> n >> m >> k;
    memset(dist, 0x3f, sizeof dist);
    
    for(int i = 1; i <= m; i ++ ) {
        int a, b, c;
        cin >> a >> b >> c;
        //代表a到b有一条权值为c的边
        edges[i] = {a, b, c};
    }
    
    bellman_ford();
    
    if(dist[n] > 0x3f3f3f3f / 2) cout << "impossible" << endl;
    else cout << dist[n] << endl;
}

---

②spfa模板(ACwing.851)

相关分析

时间复杂度： $O(m)$

适用场景： 其实spfa这个算法以他比较优越的时间复杂度，其实用在很多题目都可以，且不仅能够求带负权的最短路，在一定程度上也可以解决dijkstra的题目。并且这个算法，可以判定一个图里面是否有负环

思路： 这里的思路其实也是从上一个bellman-ford算法延申过来的。我们可以看到，上一个算法的好处就是可以知道有边限制的最短路，但是其实如果没有边的限制的话，第一个算法其实在内层循环遍历边的时候，会有很多操作本身更新不了一个点到原点的距离，但是还是进行了一个尝试更新的操作。那么spfa的话其实就是可以排除这些没有实际价值的更新操作，也就是说在$dist[j] = dist[t] + w[i] $的那一步，只有一个点能够达到这一步操作了，让这个点进入队列之中，才有机会更新其他的边，如果某个点本身压根无法更新其他边，那也就没有必要让他到队列中再去更新其他边 

完整AC代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 1e5 + 5;
bool st[N];
int dist[N], n, m;
int h[N], w[N], e[N], ne[N], idx;
queue<int> q;

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void spfa() {
    q.push(1);
    dist[1] = 0;
    st[1] = true;
    //利用类似宽搜的方法进行优化
    while(q.size()) {
        auto t = q.front();
        q.pop();
        //注意用过的点，有可能在后续更新的时候会继续用
        st[t] = false;
        
        for(int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            
            if(dist[j] > dist[t] + w[i]) {
                dist[j] = dist[t] + w[i];
                if(!st[j]) {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
}

int main() {
    memset(h, -1, sizeof h);
    memset(st, 0, sizeof st);
    memset(dist, 0x3f, sizeof dist);
    cin >> n >> m;
    
    for(int i = 1; i <= m; i ++ ) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    
    spfa();
    
    if(dist[n] > 0x3f3f3f3f / 2) cout << "impossible" << endl;
    else cout << dist[n] << endl;
    
    return 0;
}

代码相关问题

这里的话有一个问题，就是为什么一个已经被使用来更新其他点的点，从对头取出来的那一刻，他的st数组要被更新成为没有使用过，这里举一个例子，例子图如下:

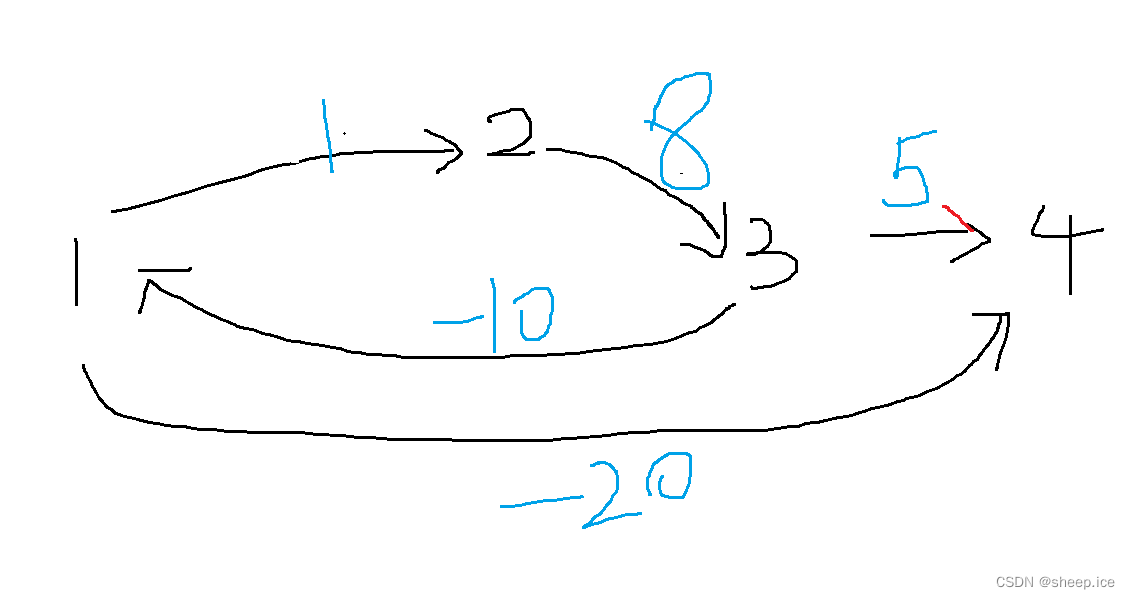
我们可以看到这个图，假设，我们在用1这个点第一次更新好1->2和1->4的距离后，不让他的st数组变为false的话，那么当3这个点用来更新1的时候，很显然从1->2->3->1一回会让整个路径变小，而我们虽然更新了一下3->1的距离，但是并没有在后面让1入队的话，那么1这个点就不会继续更新4这个点，当然这个例子有些问题，因为，我们可以一直让上方的环不断的走，让最后的1到4的路径距离不断的减少，所以希望读者有更好的例子可以举例一下。

当然，这个题，如果不专门用st代表是否访问，直接更新然后不断放点那其实就等同于bellman-ford算法了，所以还是建议这个地方能够继续好好理解一下。然后也正因为这样，spfa算法可以去判定一下是否有负环，或者是否有一个环可以让某一个路径的距离一直减小。

③spfa判断负环(ACwing. 852)

负环的定义就是一个环上边的权值全部为负数，刚开始我还一直这么认为的，其实负环应该是一个环上所有数加起来的权值和是为负数叫做负环，因此根据上面的一个分析，其实判断负环就很容易了，就看循环是不是一直跑不出来，因为不能死循环，所以我们要利用一个cnt数组，判断一下某个点走了多少次，根据抽屉原理，一旦走的次数比n大的时候，那么一定存在负环。

完整AC代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 100050, INF = 1e9 + 10;
int n, m, idx;
int h[N], e[N], ne[N], w[N];
int dist[N], cnt[N];
bool st[N];

void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++ ;
}

bool spfa() {
    queue<int> q;
    for(int i = 1; i <= n; i ++ ) {
        q.push(i);
        st[i] = true;
    }
    
    while(q.size()) {
        int t = q.front();
        q.pop();
        st[t] = false;
        for(int i = h[t]; i != -1; i = ne[i] ) {
            int j = e[i];
            
            if(dist[j] > dist[t] + w[i]) {
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;
                
                if(cnt[j] >= n) return true;
                
                if(!st[j]) {
                    st[j] = true;
                    q.push(j);
                }
            }
        }
    }
    
    return false;
}

int main() {
    cin >> n >> m;
    memset(h, -1, sizeof h);
    
    for(int i = 0; i < m; i ++ ) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    
    if(spfa()) cout << "Yes" << endl;
    else cout << "No" << endl;
    
    return 0;
}

代码问题

为什么dist数组不用初始化为正无穷？

​ 其实就是，负环必须走的那个路径是有负数产生的，且由于一个环必须满足权值为负，那么我们其实可以偷懒一下，让每次开始更新dist出现在，我们搜索的时候，第一次搜到的负数开始，然后在更新dist，如果有负环，那么这个dist是会不断减少的。这个等价于什么呢，我们可以发现，之前的题目都是从1这个点出发开始的，而负环不一定存在1这个点连接的路径上，所以其实在刚开始，队列就应该把所有点放进去，然后所有点去找负环，那也就是说从这个角度看，所有点距离本身的距离为0，那么初始化为0就是正确的！