一、前言

在之前的图论算法中有说过基本都是从一个原点出发，然后定义其他点到原点的一个距离最小值。那假设这个原点都是不固定的，而题目刚好要求去求任意两个点之间的最小距离的话，那么这个时候暴力美学就非常凸显出其独有的重要性了。那么本章总结的Floyd算法，就是能够解决这样的问题。

本章题大多来源于ACwing,欢迎大家来这个平台一起学习算法！！

二、题目汇总

①Floyd算法模板(ACwing.854)

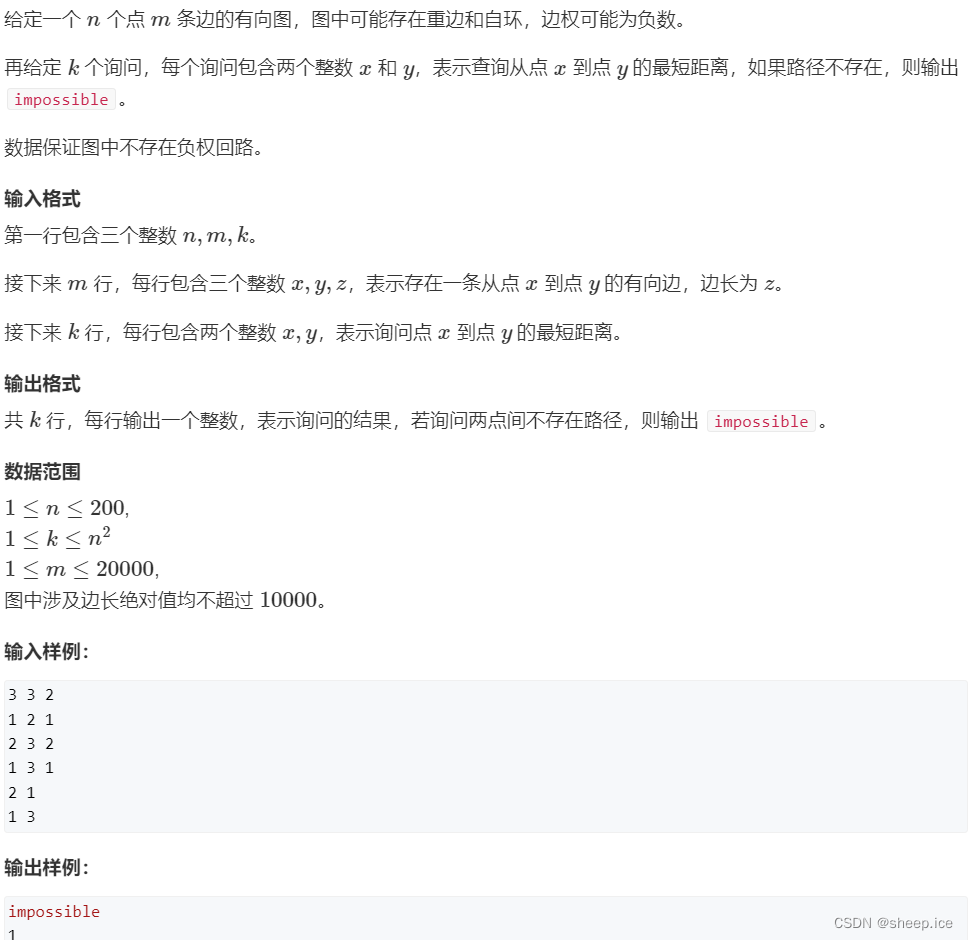
Floyd求最短路

完整AC代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int INF = 1e9;
const int N = 205;
int n, m, k;
int grid[N][N];

void floyd() {
    for(int k = 1; k <= n; k ++ ) {
        for(int i = 1; i <= n; i ++ ) {
            for(int j = 1; j <= n; j ++ ) {
                grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]);
            }
        }
    }
}

int main() {
    cin >> n >> m >> k;
    //初始化
    for(int i = 1; i <= n; i ++ ) {
        for(int j = 1; j <= n; j ++) {
            if(i == j) grid[i][j] = 0;
            else grid[i][j] = INF;
        }
    }
    
    for(int i = 1; i <= m; i ++ ) {
        int a, b, c;
        cin >> a >> b >> c;
        
        grid[a][b] = min(grid[a][b], c);
    }
    
    floyd();
    
    while(k -- ) {
        int x, y;
        cin >> x >> y;
        
        if(grid[x][y] > INF / 2) cout << "impossible" << endl;
        else cout << grid[x][y] << endl;
    }
    
    return 0;
}

相关问题

循环的顺序能不能变？

在上面的代码，我们可以看到，循环的顺序是先循环k，再循坏i，j。也就如下

void floyd() {
    for(int k = 1; k <= n; k ++ ) {
        for(int i = 1; i <= n; i ++ ) {
            for(int j = 1; j <= n; j ++ ) {
                grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]);
            }
        }
    }
}

如果把k这一层放到最内层，如下的话可以吗？

void floyd() {
    for(int i = 1; i <= n; i ++ ) {
        for(int j = 1; j <= n; j ++ ) {
            for(int k = 1; k <= n; k ++ ) {
                grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]);
            }
        }
    }
}

答案是不行的！

首先举个例子，假设有一组样例是这样的

10 4 1

2 8 1

8 9 8

9 1 10

1 10 0

2 10

上面的样例，显然从2到10的距离最短是19，但是如果按照第二种方式，最后得到的结果会是impossible的，为什么呢？从循环顺序来看，当我们要求$ g[2][10]$的时候就需要求$g[2][1]$,而在求$g[2][1]$的时候，我们发现$g[2][1]是通过g[2][9]和g[9][1]得到的 $，而如果循环把k放到内层，那么$g[2][9]$会在i=2，j=9的时候才能推出来，这样就导致$g[2][1]$不能顺利得到正确结果，也就是最后得不到一条2到10的最短距离。

其次我们应该用动态规划的思想去理解Floyd的算法。我们可以让这个算法的动态规划数组看成$f(k, i, j)$代表以前k个点为媒介的时候，从i到j这个点的最短距离。

利用dp分析的方法有下面这个图

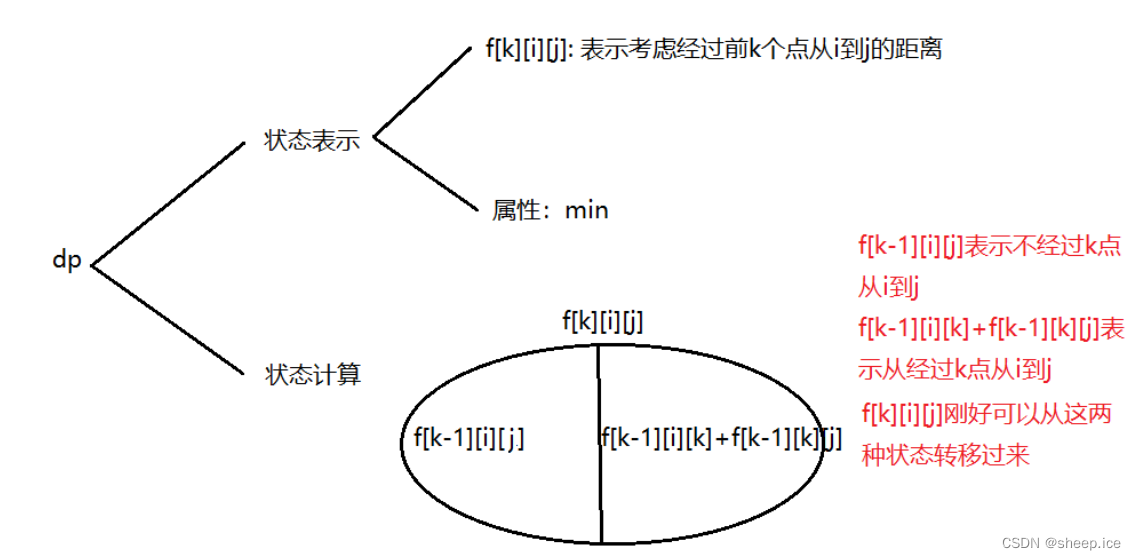
闫式dp分析