一、前言
本篇开始进行有关图论Dijkstra的题目整理,首先会整理两个模板,针对dijkstra的朴素版本和优化版本,此系列也会一直的更新,对于之后做到相关的题目,会放到此专题当中!而对于这个算法来说,一般求的是对于一些有向图,从某个点走到另外的一个终点不同路径的最小距离,注意此时有向边的权值必须为正数才行!
本章题大多来源于ACwing,欢迎大家来这个平台一起学习算法!!
二、题目汇总
①朴素版Dijkstra(ACwing 849)
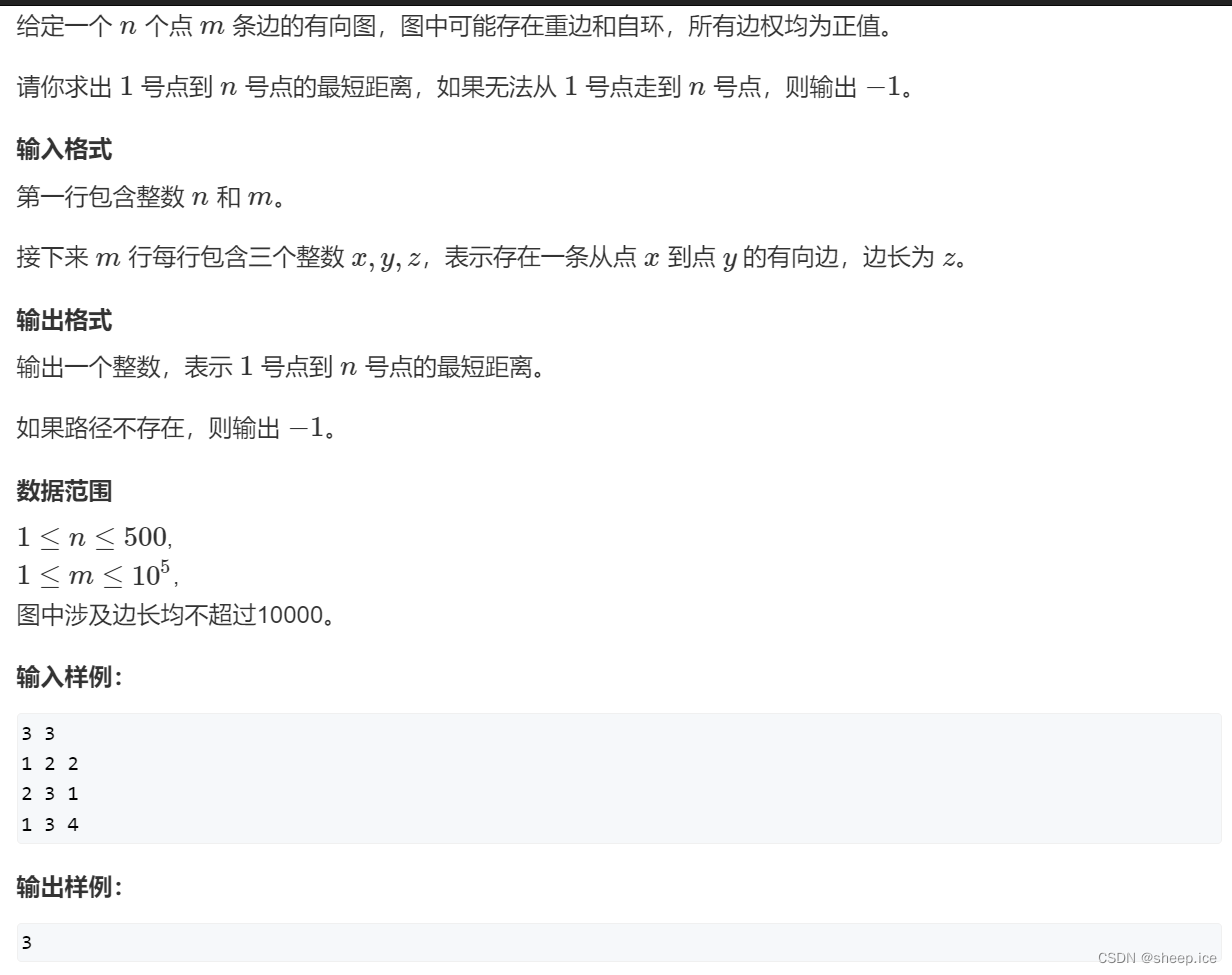
相关分析:
时间复杂度: $O(n^2)$,此处的n代表点的数量
适用场景: 题目中是稠密图,点比较少,但是边比较多。此时利用邻接矩阵存图!
思路: 朴素版本的Dijkstra的整体思路就是,从某个点(记作一号点)开始设其距离为0,然后通过与他本身距离更短的点不断的更新其他点到一号点的一个距离。外层的循环就是循环点的编号,内层的循环就是找到第一个离原点最近的那个点,然后利用那个点更新他其他边到原点最近的距离。
完整AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 505;
//邻接矩阵存图, n表示点数,m表示边数量;
int g[N][N], n, m;
//dist数组表示某个点到原点的最短距离
int dist[N];
//记录某个点有没有被更新过
bool st[N];
void dijkstra() {
//原点距离本身为0
dist[1] = 0;
//两层循环
for(int i = 1; i <= n; i ++ ) {
//哨兵,便于选点
int t = -1;
//找到没有用来更新其他点的最短距离原点的点
for(int j = 1; j <= n; j ++ ) {
if(!st[j] && (t == -1 || dist[j] < dist[t])) {
t = j;
}
}
//t这个点已经用来更新过了
st[t] = true;
//用t这个点更新一下
for(int j = 1; j <= n; j ++ ) {
dist[j] = min(dist[j], g[t][j] + dist[t]);
}
}
}
int main() {
//初始化,刚开始边都是正无穷,便于取最小,判定是否有路径
memset(g, 0x3f, sizeof g);
memset(dist, 0x3f, sizeof dist);
cin >> n >> m;
for(int i = 1; i <= m; i ++ ) {
//代表a到b有一个权值为v的边
int a, b, v;
cin >> a >> b >> v;
//可以提前排除自环
if(a != b) g[a][b] = min(g[a][b], v);
}
//进行求解
dijkstra();
//如果路径不存在,那么dist[n]还是正无穷
if(dist[n] == 0x3f3f3f3f) cout << -1 << endl;
else cout << dist[n] << endl;
return 0;
}②堆优化版Dijkstra(ACwing.850)
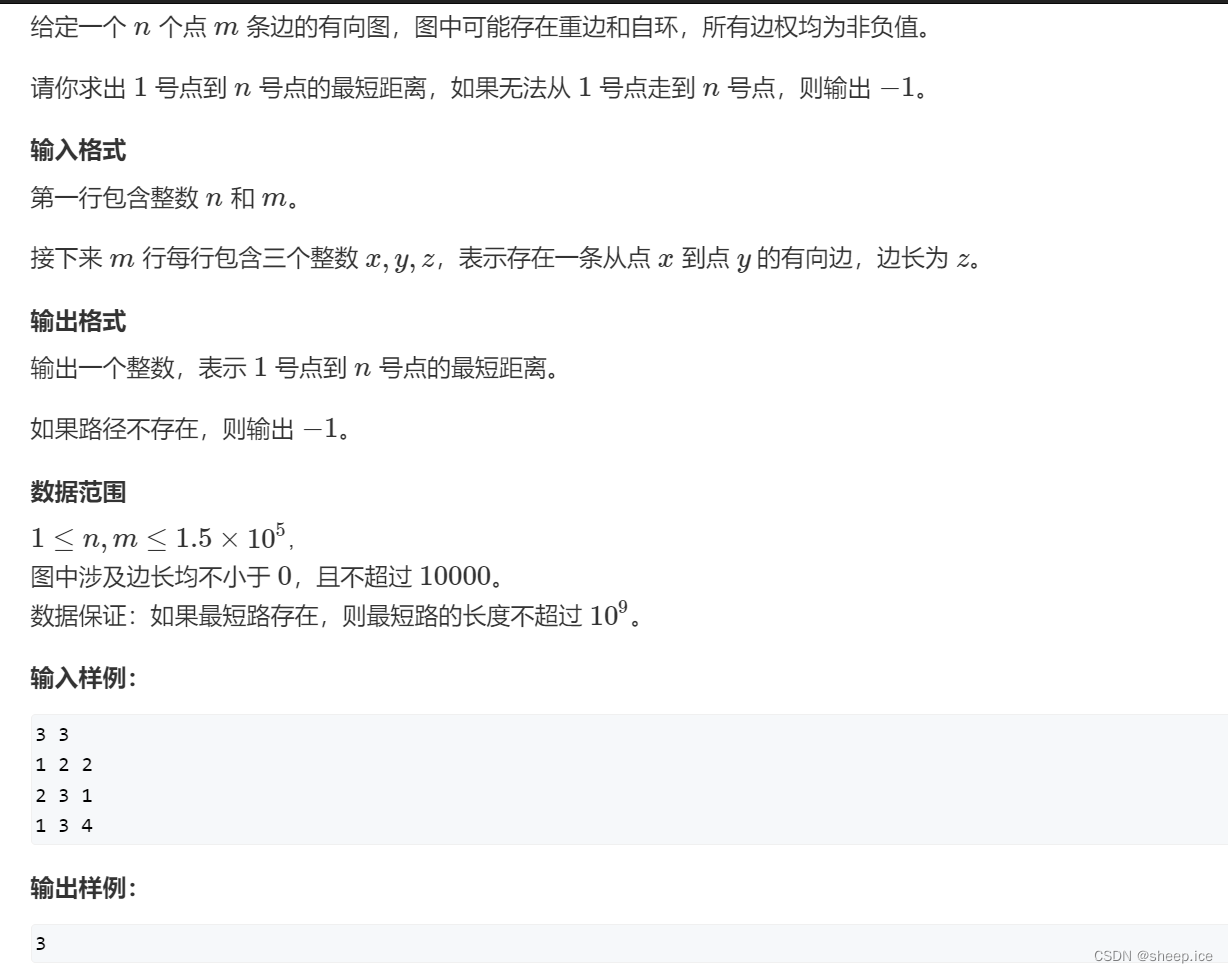
相关分析
时间复杂度: $O(mlogm)$
适用场景: 这个题目和第一个题目最大的不同就是点数变多了,而如果再使用$O(n^2)$的做法就会超时,所以需要看点数比较多,而边数能够满足时间复杂度的时候就可以使用了。
思路: 之所以有这个优化,主要是因为我们可以看到第一个解法再寻找t用来更新其他路径的时候,是利用一层循环进行更新才能保证t的那个点更新的距离是最短的,但是其实这个过程是可以利用一个数据结构–优先队列(堆)进行相关的优化的,而在堆进行查找的操作是O(1)的,只不过删除元素后,把堆调整,是需要log的时间,所以以上的时间可以被优化。
完整AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 2e5;
int m, n, dist[N];
//利用邻接表存
int h[N], e[N], ne[N], w[N], idx;
//队列放一个pair,pair第一个装距离,第二个装点编号
//因为pair默认按照第一个关键字排序
//这样可以做到排序的时候就是按照距离短进行
priority_queue<PII, vector<PII>, greater<PII> > q;
bool st[N];
//邻接表的一半添加操作,头插法
void add(int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++ ;
}
void dijkstra() {
dist[1] = 0;
//先让队列存在第一个点,第一个点的距离为0,编号是1
q.push({0, 1});
while(q.size()) {
auto t = q.top();
q.pop();
//如果此点已经更新了其他点就不用再更新
if(st[t.y]) continue;
//标记此点用来更新其他点
st[t.y] = true;
for(int i = h[t.y]; i != -1; i = ne[i]) {
int j = e[i];
//只有让某个点的距离能够更新的情况
//才把那个点放到队列,可能用来更新其他点到原点的距离
if(dist[j] > w[i] + dist[t.y]) {
dist[j] = w[i] + dist[t.y];
q.push({dist[j], j});
}
}
}
}
int main() {
//初始化操作
//距离先初始化为正无穷
//头结点开始指向空,记作-1
memset(dist, 0x3f, sizeof dist);
memset(h, -1, sizeof h);
memset(st, 0, sizeof st);
cin >> n >> m;
for(int i = 1; i <= m; i ++ ) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
dijkstra();
if(dist[n] == 0x3f3f3f3f) cout << -1 << endl;
else cout << dist[n] << endl;
return 0;
}


