区间DP

一、前言

最近写的一些相关文章，主要会整理一下相关题目，此系列会不断的更新，只要遇到了相关的题目就都会整理在一起！本篇主要针对区间DP进行相关整理。区间dp有一个特点，就是一般题目都会对一个区间进行一些处理，而此dp的状态定义也与区间相关。而整个题目的分析，采取闫式dp分析法，从状态表示，状态计算两个方面分析每一个dp题目。希望之后做到类似的题目的时候能够更快速的分析出如何解题！

本章题大多来源于ACwing,欢迎大家来这个平台一起学习算法！！

题目汇总

①ACwing 282.石子合并

注意：

本题和大家比较常见的合并果子那一个贪心题不同，因为此题必须合并相邻的两堆石子。如果合并的顺序是任意的话才能够利用贪心！

DP分析

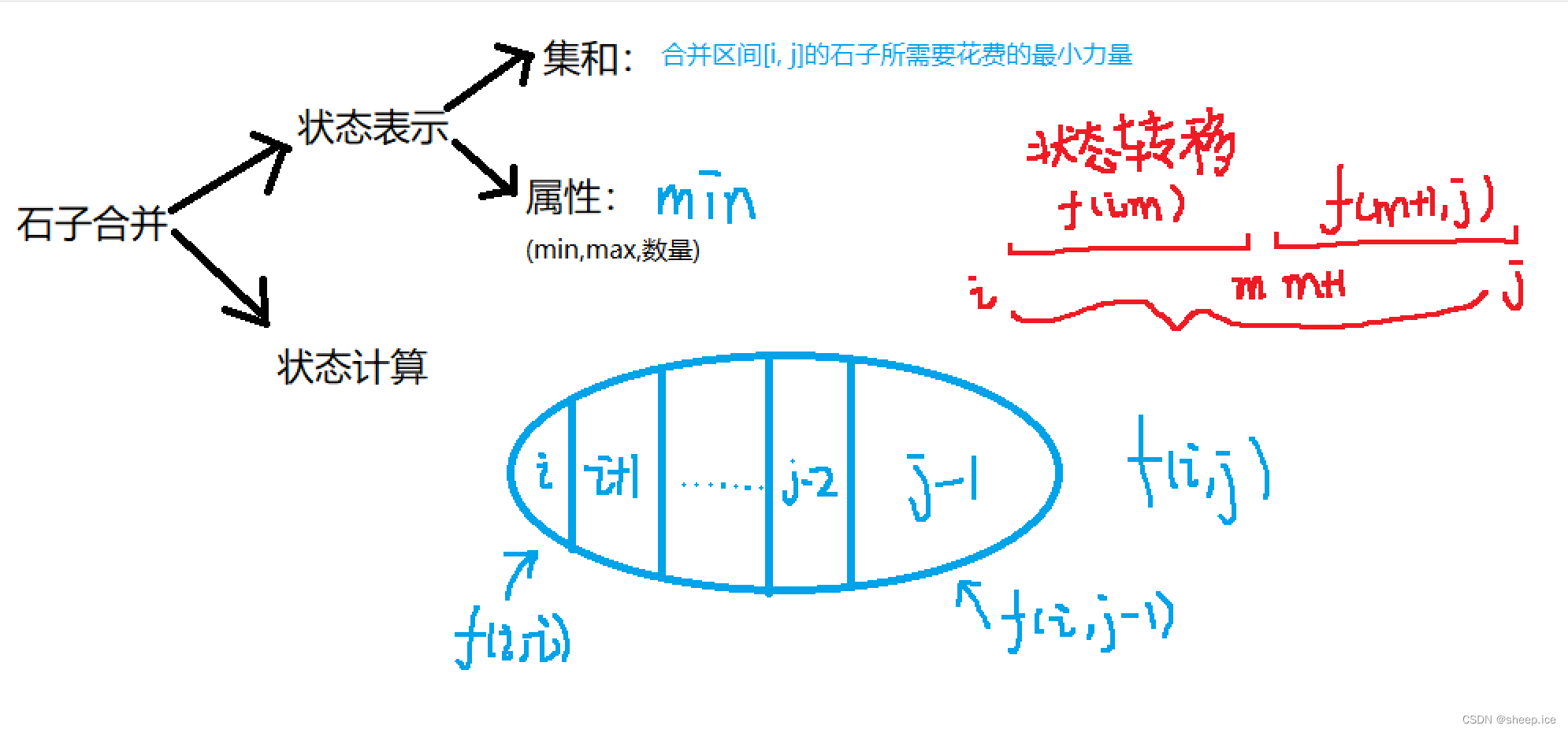
此处解释上方的一个分析方法

对于动态规划来说，如何能够正确的写出这类的题目，首先要知道，先定义一个与题目相关的状态表示，而这样的状态表示恰好表示一类集合，而这一类集合表达出来以后，是可以先考虑以集合的最后一个点作为分界点往前看。

假设我们在计算f(i, j)的时候，我们可以以j为分界点，把集合分成j - 1的子集合，状态转移中的m分界点。注意这个m所选取的区间是落在[i, j)这个区间内的。

为什么i为闭区间，j为开区间呢？

因为选i为分界点，可以分为拿第一个和后面所有为两个区间

而如果选j为分界点，就无法分成两堆了！

一旦分好这些分界点之后，就知道如何进行递推了。

状态转移

如果以m为分界点，我们要计算f(i, j)的值

$f(i, j) = min(f(i, m) + f(m + 1, j) + sum(i, j)), m \in [i, j)$

其中sum(i, j)表示[i, j]区间所有果子合并需要花费的体力值，这个也就是合并两段区间所需要的体力值！而因为这个是一个区间求和的问题，因此再计算sum的时候就可以利用前缀和进行一个优化了！

最后结果就是：f(1,n)

初始化

对于初始化来说，有下面情况

i == j : 就是合并一个石子的最小花费为0(因为不需要合并)

i < j : 最小花费初始化为$+\infty$,因为要求最小值，所以可以初始成一个很大的数，这里不能说初始化为0，因为0代表无花费，这样的话怎么推导，都是最小为0，那么最后的答案肯定是0

完整AC代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 305, INF = 0x3f3f3f3f;
//初始化1
int f[N][N];
//前缀和数组
int sum[N];

int main() {
    int n;
    cin >> n;
    for(int i = 1; i <= n; i ++ ){
        cin >> sum[i];
        sum[i] += sum[i - 1];
    }
    
    //先枚举可能的区间长度
    for(int len = 2; len <= n; len ++ ) {
        //左端点为i，右端点为i + len - 1;
        //满足右端点在n内就可以满足左端点范围
        for(int i = 1; i + len - 1 <= n; i ++ ) {
            int l = i, r = i + len - 1;
            //初始化2
            f[l][r] = INF;
            
            //枚举分界点m
            for(int m = l; m < r; m ++ ) {
                //状态转移
                f[l][r] = min(f[l][r], f[l][m] + f[m + 1][r] + sum[r] - sum[l - 1]);
            }
        }
    }
    
    cout << f[1][n] << endl;
    
    return 0;
}