一、前言
字典树是一个比较神奇的东西。试想如果我们要用程序去存一些字符串,但是相同的字符不能放在不同的空间里面,比如有两个字符串abc,abf,我们发现ab是相同的,就需要我们把他们存在一个数组空间?我们应该怎么做到呢?再来就是为什么叫字典树呢,其实很形象的说明了他的存储方式,就是字典。我们在查字典的时候,都会先查一个单词的首字母,然后在对应的地方继续依次查后面的字母。也就是我们可以利用数组完成这样的存储
但是由于一般数组的空间有限,字典树会占据很多的空间,一个abc就占用了3个单位空间,所以在用的时候是需要注意一下数据范围,是否能够不爆空间!
二、相关操作
①前期变量定义
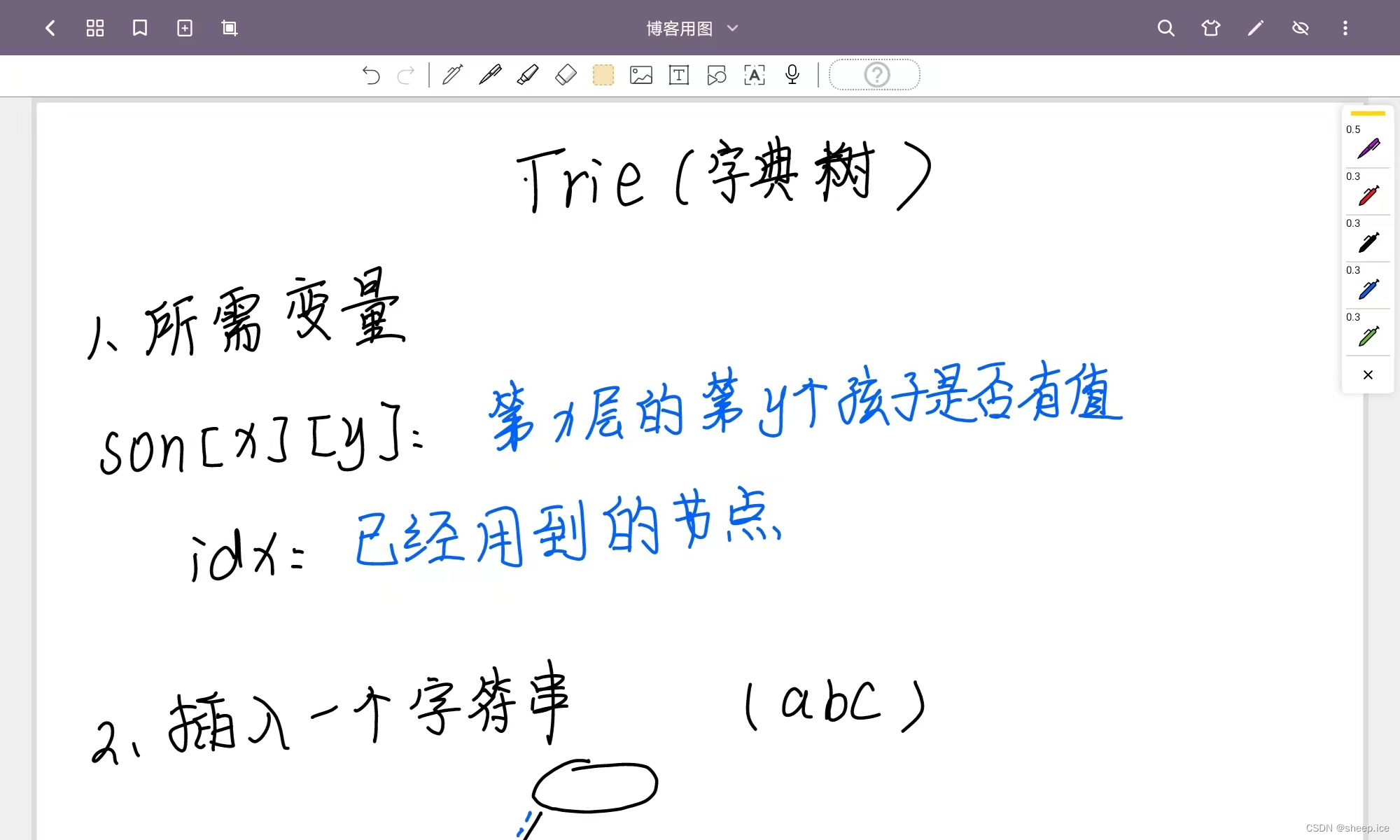
字典树需要一个二维数组空间,叫做son,为什么这么称呢。因为我们整个树的根节点我们用idx=0来表示。这个点是整个树的头,他有无数的儿子,儿子又有无数的儿子。所以我们亲切的称后续的节点为一个儿子
而son的定义其实就是每一个x都会对应有y个儿子,无论我们是插入操作还是查询操作,为了满足不浪费多余的空间,我们都需要进行首先的判断,作为第x的父亲是否已经存在y这个节点,如果不存在,就给他一个儿子,如果存在,就一视同仁为一个儿子。
②插入一个字符串
假设我们树中的字符串全是小写字母,那我们的儿子其实只可能有26个,所以在开数组的时候就可以开: int $son[N][26]$,而我们后面的例题主要以这个为主。

上面我觉得插入讲得比较清楚了,所以直接贴一个代码好了
void insert(string ss) {
int sz = ss.size();
int p = 0;
for(int i = 0; i < sz; i ++ ) {
int u = ss[i] - 'a';
//如果没有这个儿子就给他一个儿子
if(son[p][u] == 0) son[p][u] = ++idx;
//不管有没有儿子,p指针都会朝向儿子或者新建点走
//一旦p走向新建的点,其实就代表后面的所有点都是新建的
p = son[p][u];
}
}③查询一个字符串
查询其实和构建是差不多的,就是看我们要查询的字符串是否能够完全的走完构建好的字符串,至于查询,结合后面的题目,大家可以理解,直接贴一个小小的代码。
int query(string ss) {
int sz = ss.size();
int p = 0;
for(int i = 0; i < sz; i ++ ) {
int u = ss[i] - 'a';
if(son[p][u] == 0) return 0;
p = son[p][u];
}
return cnt[p];
}三、相关题目
题目一

上面的题目就是比较经典的,查询字串出现次数的题目,在我们构建树的时候,我们另外开一个cnt数组,记录一个字符串最后那个字母所在的位置出现了多少个就能解决这个题目了。可以直接看一下完整的代码。
完整AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100005;
int son[N][26], cnt[N], idx;
void insrt(string ss) {
int sz = ss.size();
int p = 0;
for(int i = 0; i < sz; i ++ ){
int u = ss[i] - 'a';
if(son[p][u] == 0) son[p][u] = ++ idx;
p = son[p][u];
}
cnt[p] ++ ;
}
int query(string ss) {
int sz = ss.size();
int p = 0;
for(int i = 0; i < sz; i ++ ) {
int u = ss[i] - 'a';
if(son[p][u] == 0) return 0;
p = son[p][u];
}
return cnt[p];
}
int main() {
int n;
cin >> n;
while (n -- ) {
string op, in;
cin >> op >> in;
if(op == "I") {
insrt(in);
}
else {
cout << query(in) << endl;
}
}
return 0;
}题目二

这个题目比较的好玩,其实这个题目就是在表述一个二叉树,具体的思路如图解
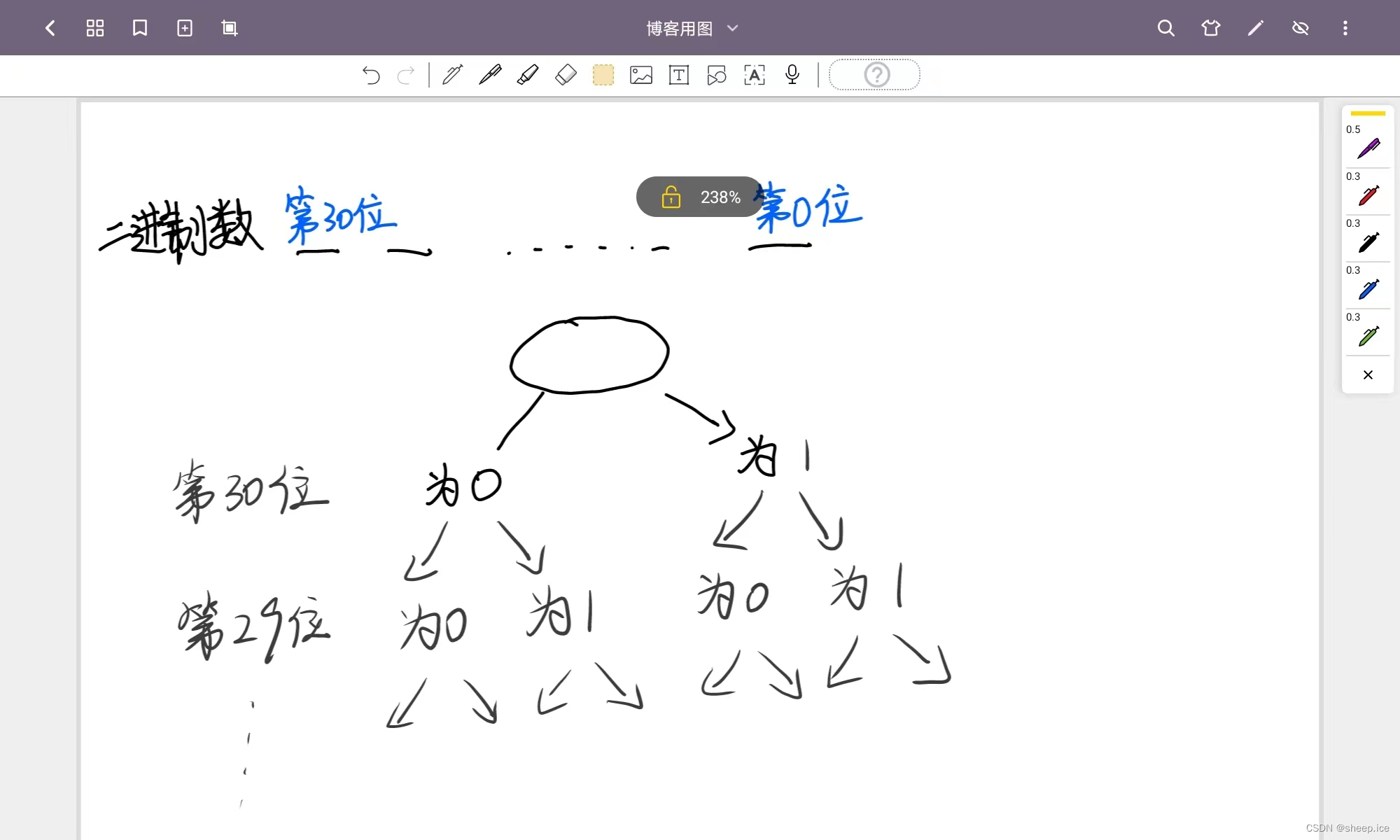
我们都知道一个二进制数异或起来,相同为0,不同为1,那其实就是再告诉我们,我们在不断建树的过程中,可以用待插入元素,与树中的元素比较,每次去看相同位下有没有和本身不同位的儿子,如果有的话,我们就可以忘那个儿子的路径走。
比如下图:

依次插入5,3,4并且寻找最大异或的元素,
再插入4的时候,先寻找最大异或,我们发现4的二进制是100
对于1这一位,先找有没有0儿子,恰好3的第一位为0,一次类推,他和3抑或能够得到最大的异或值7(111);
完整AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 100050, M = 31 * N;
//因为儿子只可能有0,1两个选项
int son[M][2], idx = 0;
void insert(int num) {
int p = 0;
//体重说最多有31位
for(int i = 30; i >= 0; i -- ) {
int u = (num >> i) & 1;
if(son[p][u] == 0) son[p][u] = ++idx;
p = son[p][u];
}
}
int query(int num) {
int p = 0, ret = 0;
for(int i = 30; i >= 0; i -- ) {
int u = (num >> i) & 1;
//如果有不同的儿子
if(son[p][!u] != 0) {
ret = ret * 2 + !u;
p = son[p][!u];
}
//如果没有不同的儿子
else {
ret = ret * 2 + u;
p = son[p][u];
}
}
return ret;
}
int main() {
int m, num;
cin >> m;
int ans = 0;
while (m -- ) {
cin >> num;
insert(num);
ans = max(num ^ query(num), ans);
}
cout << ans << endl;
return 0;
}


