一、前言

这一章记录的是自己学习KMP算法的一个笔记吧。我觉得KMP虽然目前没有用到相关的算法，但是他的思想很妙，很多人在刚开始会非常不理解这个算法的由来。而我也是写了好几遍才能够真的说掌握了一些KMP算法。其实主要记住一点就是，KMP完成了字符串与本身进行比较的一个思路。

所有字符串下标从1开始

二、相关操作

①相关变量的定义

说真的我觉得相关一些数组的定义是整个这个算法的核心

首先就是题目给的两个串，一个比较长的叫做模式串，另外一个叫做子串，题目的要求就是子串在模式串出现的位置或者出现的次数

我们再看最难理解的一个ne数组的定义，最长子串的公共前后缀长度

其实这个地方需要加上一个定义，假设ne[X], 这个其实代表的是，子串从1-X位置的字符串的最长公共前后缀的长度。这里要说明的是，前后缀是什么

前缀:包含字符串首字母的连续子串
后缀:包含字符串尾字母的连续子串

比如字符串：abc

前缀有: a ab

后缀有: c bc

②ne数组的求解

搞清楚了前后缀之后，如果我们要去求ne数组怎么求呢？

假设我们有一个字符串：abcabf

a : 0

ab : 0

abc : 0

abca : a为公共前后缀 1

abcab: ab为公共前后缀 2

abcabf: 0

而上方求出这样一个数组便是去比较p字符串的本身,匹配图如下：

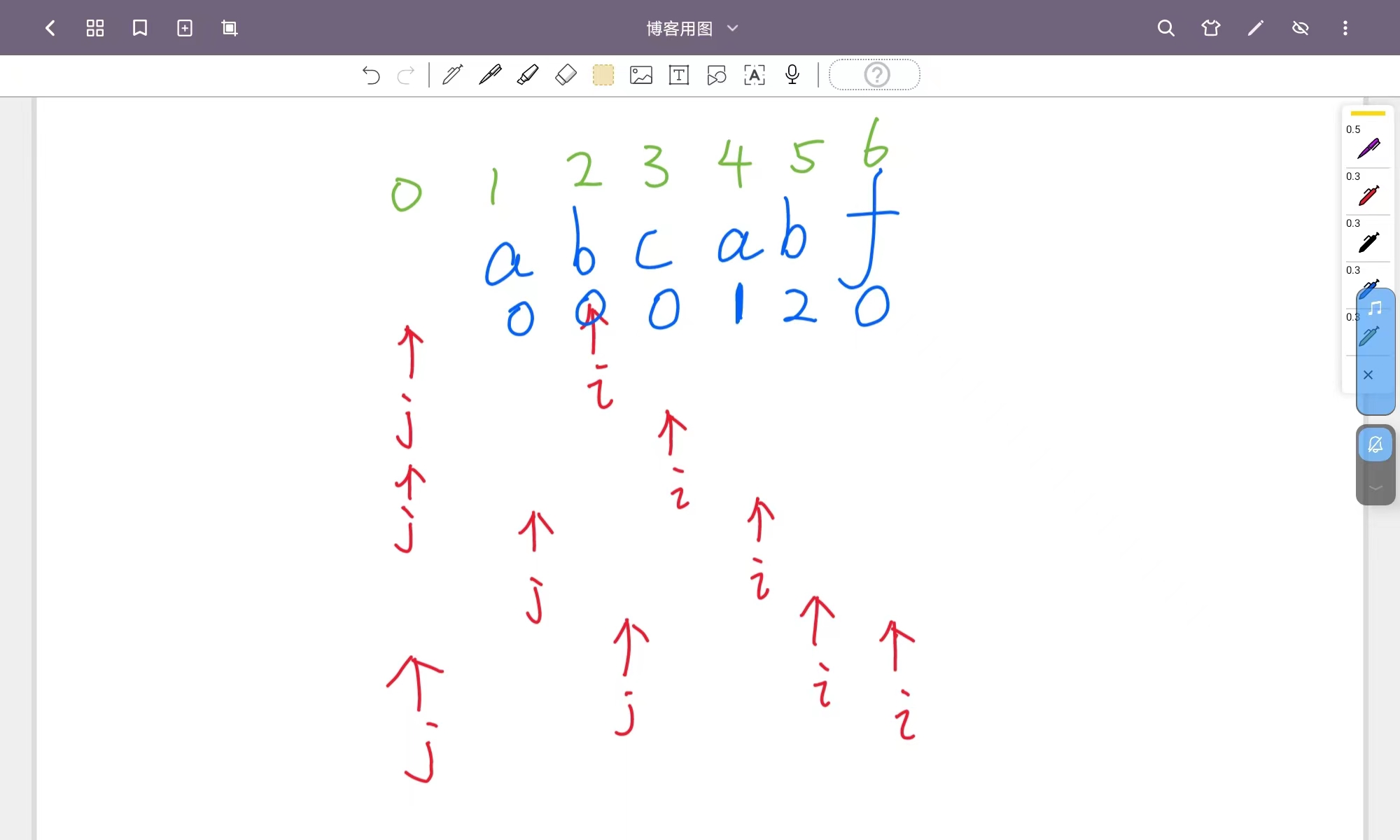
代码如下：

for(int i = 2, j = 0; i <= n; i ++ ) {
        while(j != 0 && p[j + 1] != p[i]) j = ne[j];
        if(p[j + 1] == p[i]) j ++ ;
        ne[i] = j;
    }

③字符串匹配

为什么求出一个ne数组就可以拿来进行匹配了呢？

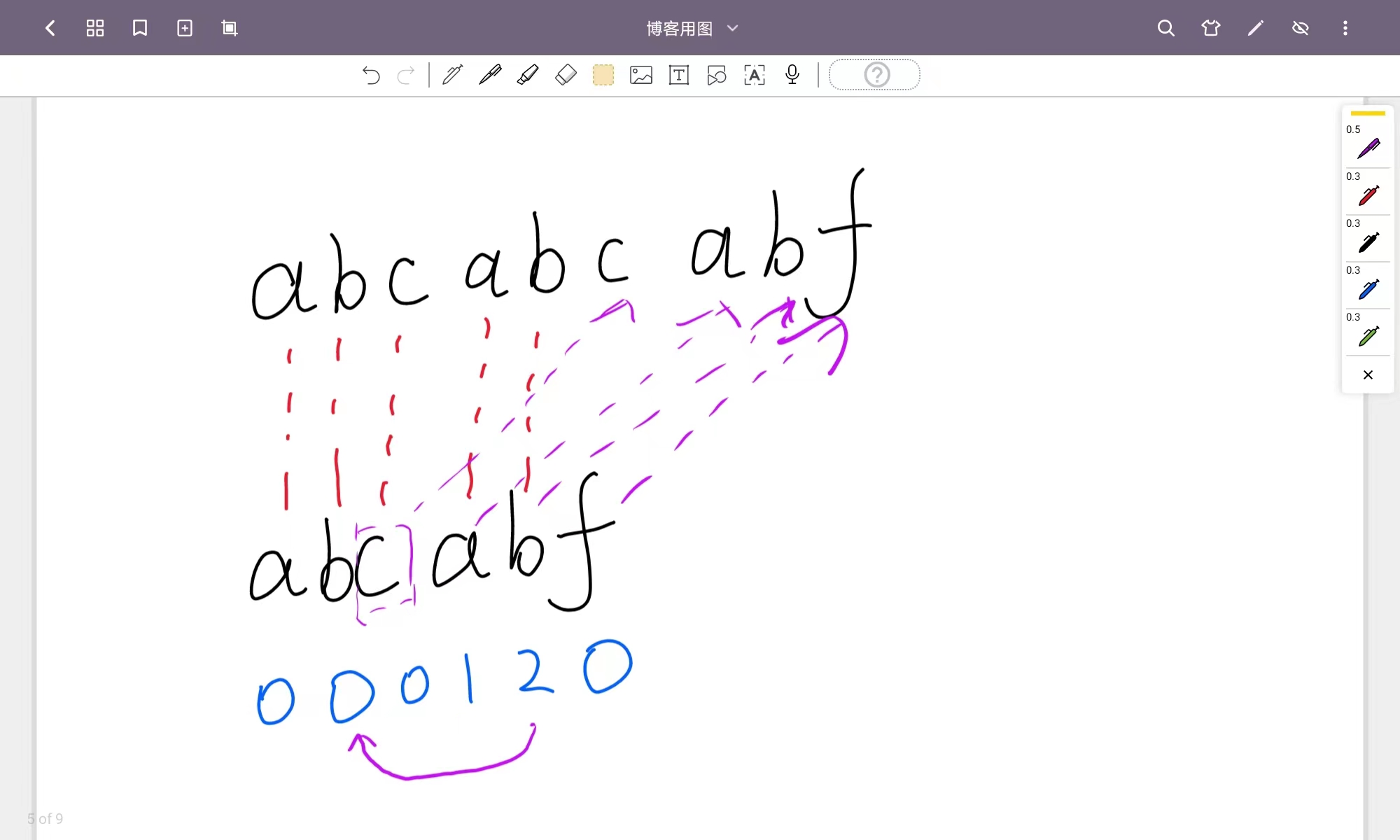
这个是我最常用进行的一个理解图

我们可以看到有两个子串

q : abcabcabf
p : abcabf

当p匹配到f的时候发现不相等了，那么子串p重新开始匹配的位置是由ne数组进行指示的，f位置前一个位置是b,b的ne值为2，代表此位置的公共前后缀的长度为2，那么我们需要先回到2的位置，也就是p串中的b位置，再看b后面的c是否与上面串相等。相等之后继续往后推移匹配p的串的指针j，知道j指针的值等于p的长度，说明已经匹配成功了。

上面之所以能进行，其实就是因为，p利用ne指针去指示已经匹配过的前缀，我们不再进行重新匹配，而是从匹配好的前缀再重新开始，也就是说，abf和q串的abc字串不相等了，但是abc已经完全匹配好了ab后缀，那我的p串刚好有个ab前缀，那我们直接从ab这个前缀的位置再继续往后匹配，这样就避免了重复匹配的时间复杂度！

三、相关题目

完整AC代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100050, M = 10 * N;
char p[N], q[M];
int ne[N];

int main() {
    //进行相关输入
    int n, m;
    cin >> n >> (p + 1) >> m >> (q + 1);
    
    //先进性ne数组的求解
    for(int i = 2, j = 0; i <= n; i ++ ) {
        while(j != 0 && p[j + 1] != p[i]) j = ne[j];
        if(p[j + 1] == p[i]) j ++ ;
        ne[i] = j;
    }
    
    //进行字符串的匹配
    for(int i = 1, j = 0; i <= m; i ++ ) {
        while(j != 0 && p[j + 1] != q[i]) j = ne[j];
        if(p[j + 1] == q[i]) j ++ ;
        if(j == n) {
            cout << i - n << " ";
            j = ne[j];
        }
    }
    
    return 0;
}