模拟堆

一、前言

本篇文章主要以小根堆为例子，做一些有关小根堆的知识点笔记，前面主要就是堆排序，后面呢是一个题目的相关介绍，由于那个题目的特殊性，所以不多加赘述，这一篇主要是以堆能够实现的一些操作为例子，记录一下堆的一些应用。

二、理解

本篇主要受众是已经建立在知道二叉树的建立的基础上，进行堆的记录。如果不太了解二叉树的uu们可以先去了解一下二叉树的建立，知道左右孩子的节点是怎么表示的，然后食用一下这篇文章。

堆呢，其实原型就是一颗完全二叉树，我们知道，完全二叉树必须保证树儿子的完整性，即一个节点为x的父亲，如果他有孩子，那么他左右孩子的节点位置一定为2x和(2x+ 1)，而整个树的根节点坐标从1开始计算！

而堆其实分为小根堆和大根堆。以小根堆为主要例子介绍。小根小根，就是根都是小的，也就是一个节点如果有孩子，那么他在他本身和他孩子中间，他是最小的。即是我们的小根堆。至于小根堆，以下面的图做例子，相信大家能够更加清晰的知道了。

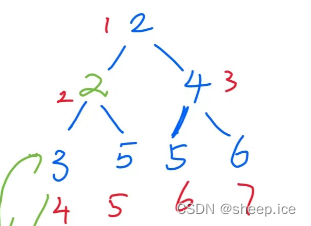
上图就是一个小根堆，而红颜色代表着每一个节点的坐标。

三、堆的相关函数

我觉得还是应该先以堆的相关函数为例子然后在进行后续堆的基本操作的讲解

①定义相关变量

const int N = 100050;
int h[N]; //存储堆的元素
int sz = 0; //表示堆的大小

②down函数

如果有一些节点发生了变化，可能会导致节点需要向下调整到合适的位置

void down(int u) {
    //记录节点和孩子谁最小，小的会到父亲的位置，成为根
    int t = u;
    //如果左孩子存在，并且比根小的话
    if(2*u <= sz && h[t] > h[2*u]) t = 2*u;
    //如果有孩子存在，并且比根和左孩子小的话
    if(2*u+1 <= sz && h[t] > h[2*u+1]) t = 2*u+1;
    //如果此时记录的t不等于u的话
    if(t != u) {
        swap(h[t], h[u]);
    	//递归的处理一下后续的节点
    	down(t);
    }
}

③up函数

如果有一些节点发生了变化，可能会导致节点需要向上调整到合适的位置，而向上调整与向下不同的是，向上调整的时候，只需要跟根节点进行比较就好，因为为了满足小根堆的需求，其中孩子变化了，但是在之前一个状态下，根还是保证最小。

void up(int u) {
    //当根节点比变化的孩子大，就让他向上调整
    while(u / 2 > 0 && h[u / 2] > h[u]) {
        swap(h[u / 2], h[u]);
        u /= 2;
    }
}

四、堆的基本操作

通过堆相关函数的介绍下面其实就是函数的拼凑了

①构建一个堆

这里有一个比较巧的方法，无论是什么样的小根堆，如果他含有n个元素，那么叶子节点(没有孩子节点层)的上一层最后一个存有元素的父亲节点为n / 2,这个结论大家可以直接记住。所以我们在构建堆的时候，我们只需要从节点为n / 2处开始向上调整节点，每个节点都往下down一遍就可以建立一个堆。

//这个操作可以把一个存有元素的一维数组，按照堆的节点顺序排列
for(int i = n / 2; i > 0; i -- ) {
    down(i);
}

②向堆里面插入一个元素

这里有个技巧就是下面几个点

• 将插入的元素先插入在堆的最后
• 利用up函数向上调整一遍

h[++sz] = val;
//向上调整堆的最后一个元素
up(sz);

③删除堆中的元素

• 将待删除的元素和堆中最后一个元素
• up调整一遍
• down调整一遍

其中后面两个步骤只会进行其中一个，因为调整后，要不然就是比其父亲小，要不然就比孩子大。

swap(h[k], h[sz]);
sz--;
up(k);
down(k);

④修改堆中的某个元素值

和第三个操作类似

• 修改堆中元素值
• up调整一遍
• down调整一遍

h[k] = val;
up(k);
down(k);

⑤输出堆中的最小值

• 直接输出堆顶元素就好

cout << h[1] << endl;

不难发现，其实整个堆的调整就是类似打拳皇一样，我们先熟知每一个英雄他有什么技能，然后根据不同的需求，利用我们已知的技能，打出不同的组合技能，最终KO对方。而我们就是要利用组合起来的函数AC相关的算法题。还是很好玩的！

五、相关题目

题目一.堆排序

能够利用堆排序主要的原因就是小根堆能够维护我们整个堆中的最小值。当最小值被输出之后，我们删除堆顶元素，然后不断的输出新的堆顶元素，我们就可以完成这一个题目。所以只需要利用四中的①③⑤组合技我们就可以AC掉了

完整AC代码

#include<bits/stdc++.h>
using namespace std;
const int N = 100005;
int m, n;
int sz, h[N];

void down(int x) {
    int t = x;
    //左子树存在且比节点小
    if(2 * x <= sz && h[2 * x] < h[t]) t = 2 * x;
    //右子树存在且比节点小
    if(2 * x + 1 <= sz && h[2 * x + 1] < h[t]) t = 2 * x + 1;
    if(t != x) {
        swap(h[t], h[x]);
        down(t);
    }
}

int main() {
    cin >> n >> m;
    sz = n;
    for(int i = 1; i <= n; i++) cin >> h[i];
    for(int i = n / 2; i; i--) down(i);
    while(m--) {
        cout << h[1] << " ";
        h[1] = h[sz--];
        down(1);
    }
    return 0;
}

题目二

这个题目因为要记录一下第k个插入数的位置，所以大家可以直接用结构体装一下每个节点是第几个插入的，但是为了快速，是可以类似利用数组去模拟哈希表的方式进行实现，因为可能会有些难理解。我写了相关的注释在代码中，可以量力理解一下。

//ph[k]表示第k个插入的节点在堆中的下标，hp[k]表示堆中第k个节点是第几个插入的数。

#include<bits/stdc++.h>
using namespace std;
const int N = 100005;
int ph[N], hp[N], h[N];
//m代表第m个插入的数，cnt代表整个堆的大小
int m, cnt;
//这个swap就实现了不仅元素交换了，节点对应是第几个插入的数也被交换了！
void heap_swap(int a, int b) {
    //交换第某个插入的数的堆中下标
    swap(ph[hp[a]], ph[hp[b]]);
    //交换堆中某个节点代表插入的数
    swap(hp[a], hp[b]);
    //交换堆中的两个位置的值
    swap(h[a], h[b]);
}

//下传操作
void down(int x) {
    int t = x;
    if(2 * x <= cnt && h[2 * x] < h[t]) t = 2 * x;
    if(2 * x + 1 <= cnt && h[2 * x + 1] < h[t]) t = 2 * x + 1;
    if(t != x) {
        heap_swap(t, x);
        down(t);
    }
}

//上传操作
void up(int x) {
    while(x / 2 && h[x / 2] > h[x]) {
        heap_swap(x, x / 2);
        x >>= 1;
    }
}

int main() {
    int num, k, n;
    cin >> n;
    string op;
    while(n--) {
        cin >> op;
        //插入操作
        if(op == "I") {
            cin >> num;
            cnt++; m++;
            h[cnt] = num; hp[cnt] = m; ph[m] = cnt;
            up(cnt);
        }
        //输出最小值
        else if(op == "PM") {
            // cout << n << endl;
            cout << h[1] << endl;
        }
        //删除最小值
        else if(op == "DM") {
            heap_swap(1, cnt);
            cnt--;
            down(1);
        }
        //删除第k个插入的数
        else if(op == "D") {
            cin >> k;
            //必须先保存一个位置，否则有可能在交换过程直接交换了指针位置，导致答案错误！！
            k = ph[k];
            heap_swap(k, cnt);
            cnt--;
            up(k);
            down(k);
        }
        //修改第k个插入的数为num
        else {
            cin >> k >> num;
            int id = ph[k];
            h[id] = num;
            up(id);
            down(id);
        }
    }
    return 0;
}

作者：sheepice
链接：https://www.acwing.com/activity/content/code/content/3438577/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。