离散化操作

一、离散化操作

什么是离散化操作，这里给一个简单的解答。

假设给你一个数组，元素有1,2,200,30000,400000。按照元素的个数，将最终的数组变成1,2,3,4,5的操作就是离散化。离散化的操作有什么好处呢？

如果数据非常大，但是元素的个数非常小。我们离散化操作就会节省空间，同时通过这样的操作能够让我们优化时间复杂度！

二、实现方法

为了满足这样的要求(假设有n个数)，我们只需要让每一个数对应一个下标，而这个下标就是离散化他对应的区间$[1,n]$里面的某一个数！这里主要采用c++的实现操作！下面是具体的实现方法

①开一个vector数组

因为后面需要用到库函数，所以会更方便解题，但是其实用哈希表对应也是可以的！

vector<int> allis;

②数据放入数组之中

allis.push_back(x);

③排序之后去重

去重的目的只为了之后在找数的时候没有重复的数！(其实不去重可能也可以过)

//排序去重
    sort(allis.begin(), allis.end());
//去重的库函数
    allis.erase(unique(allis.begin(), allis.end()), allis.end());

④查找数所在的位置，最后返回应该映射的那一个数

这里也用了库函数，但是其实就是一个简单的二分，因为排序之后的数组是递增的，所以二分查找加快速度！

int finds(int x) {
    int id;
    //找到第一个大于等于x的数
    //加1是为了让下标从1开始
    id = lower_bound(allis.begin(), allis.end(), x) - allis.begin() + 1;
    return id;
}

④举例分析

假设给你一个数组，元素有1,200,2。我们的第三步操作就会让这个数组变成，1,2,200。假设后续操作遍历需要200的时候，我们就会先利用finds函数，返回3，从而，从头开始遍历的时候数组就会呈现出1，3，2的形式。

三、例题

（1）例题1：区间求和

分析

这一题乍一看其实就是一个前缀和，然后最后区间查询用前缀和的思想就好了。但是本题的难点就在区间和数的范围都是几乎接近了一个int的大小，如果我们直接用前缀和，从头到尾遍历一遍，首先数组不可能开那么大，其次是即使是O(N)的时间复杂度，因为N过大，也必然会超时。但是我们发现，n和m的值比较的小，所以从他们入手，把我们所有输入的数都进行一个离散化，最后其实就相当于最多求一个(n + 2m)那么多次的一个前缀和！因为输入的数字有n个，然后有2m个断点值(左端点和右端点)。因此如果我们把他们转化到一个非常小的区间去求前缀和，就变得非常的简单！所以套用之前的离散化操作，这里直接给出代码！

代码

#include<bits/stdc++.h>
using namespace std;
const int N = 300005;

typedef pair<int, int> PII;

vector<int> allis;
vector<PII> add, query;
int a[N], sum[N];
int n, m;
int finds(int x) {}
    int id;
    id = lower_bound(allis.begin(), allis.end(), x) - allis.begin() + 1;
    return id;
    }

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i++) {
        int x, c;
        cin >> x >> c;
        allis.push_back(x);
        add.push_back( {x, c} );
        }
    for(int i = 1; i <= m; i++) {
        int l, r;
        cin >> l >> r;
        allis.push_back(l);
        allis.push_back(r);
        query.push_back( {l, r} );
        }
    
    //排序去重
    sort(allis.begin(), allis.end());
    allis.erase(unique(allis.begin(), allis.end()), allis.end());
    
    // for(auto alli : allis) cout << alli << " ";
    
    //处理插入
    for(auto item : add) {}
        int s = finds(item.first);
        a[s] += item.second;
        }
    
    //前缀和
    for(int i = 1; i <= allis.size(); i++) {
        sum[i] = sum[i - 1] + a[i];
        }
    
    //查询
    for(auto item : query) {
        int l = finds(item.first), r = finds(item.second);
        int ans = 0;
        ans = sum[r] - sum[l - 1];
        cout << ans << endl;
        }
    return 0;
}

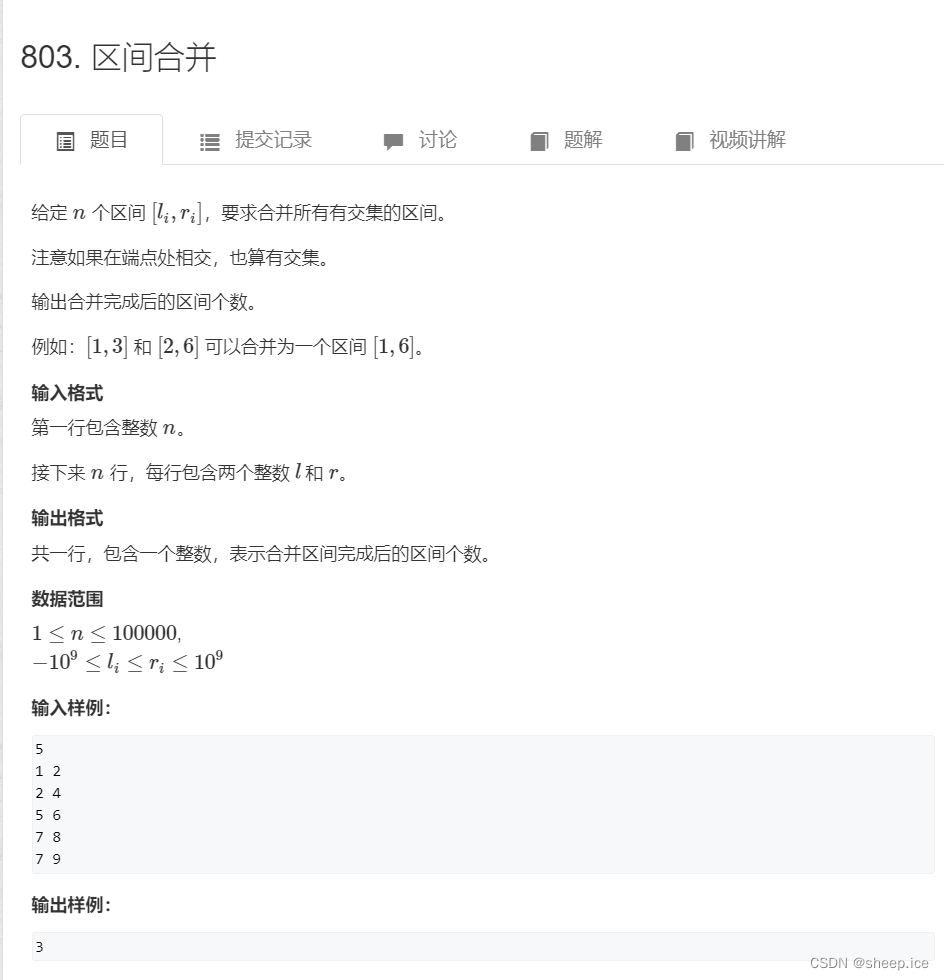
（2）例题2：区间合并

分析

因为区间合并的相关知识已经写过博客了，对区间合并不了解的uu们，可以点击这里去看看区间合并的刷题。那么这题就是在区间合并的前提下，加上一个离散化操作，所以非常的简单哈！

代码

#include<bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;
const int N = 200000 + 10;
PII p[N];

vector<int> allis;
vector<PII> query;

int finds(int x) {
    return lower_bound(allis.begin(), allis.end(), x) - allis.begin() + 1;
}

int main() {
    int n;
    cin >> n;
    int count = 0;
    for(int i = 1; i <= n; i++) {
        int l, r;
        cin >> l >> r;
        allis.push_back(l);
        allis.push_back(r);
        query.push_back({l, r});
    }
    //去重排序
    sort(allis.begin(), allis.end());
    allis.erase(unique(allis.begin(), allis.end()), allis.end());
    int t = 0;
    for(auto item : query) {
        int l = finds(item.first), r = finds(item.second);
        p[t++] = {l, r};
    }
    //这个地方不能用sort(p.begin(),p.end());
    sort(p, p + t);
    int st = -1, ed = -1;
    for(int i = 0; i < t; i++) {
        if(p[i].first <= ed) ed = max(ed, p[i].second);
        else {
            count++;
            st = p[i].first;
            ed = p[i].second;
        }
    }
    cout << count << endl;
}