一、树状数组的初学
之前学习过前缀和和差分的一些知识就觉得挺神奇的,然后昨天刷到力扣的每日一题之后发现,好像==树状数组==在多区间的修改和查询方面很神奇,包括之后要学习的==线段树==(能解决所有树状数组的问题)可能会更加有收获吧。😁😁
二、一些小小的理解
①lowbit的理解
在线段数组里面有这么一个重要的函数,也是能够构造整个树状数组的核心吧!代码只有一行,但是对于我这种萌新来说,刚开始还是很难理解的。代码如下:
//寻找一个数最低位的1
int lowbit(int x) {
return x & -x;
}举个比较简单的例子,一个数为3,他的二进制表示为11,那么根据负数二进制的要求,-3的二进制,我们先求他的反码为00,最后+1得到补码为01,最后让11 & 01 便取得 01,也就是最低位的第一个1,大家可以试一下,利用这个函数,最后得到的结果一定只会含有一个1在整个数里面;
三、树状数组的构建
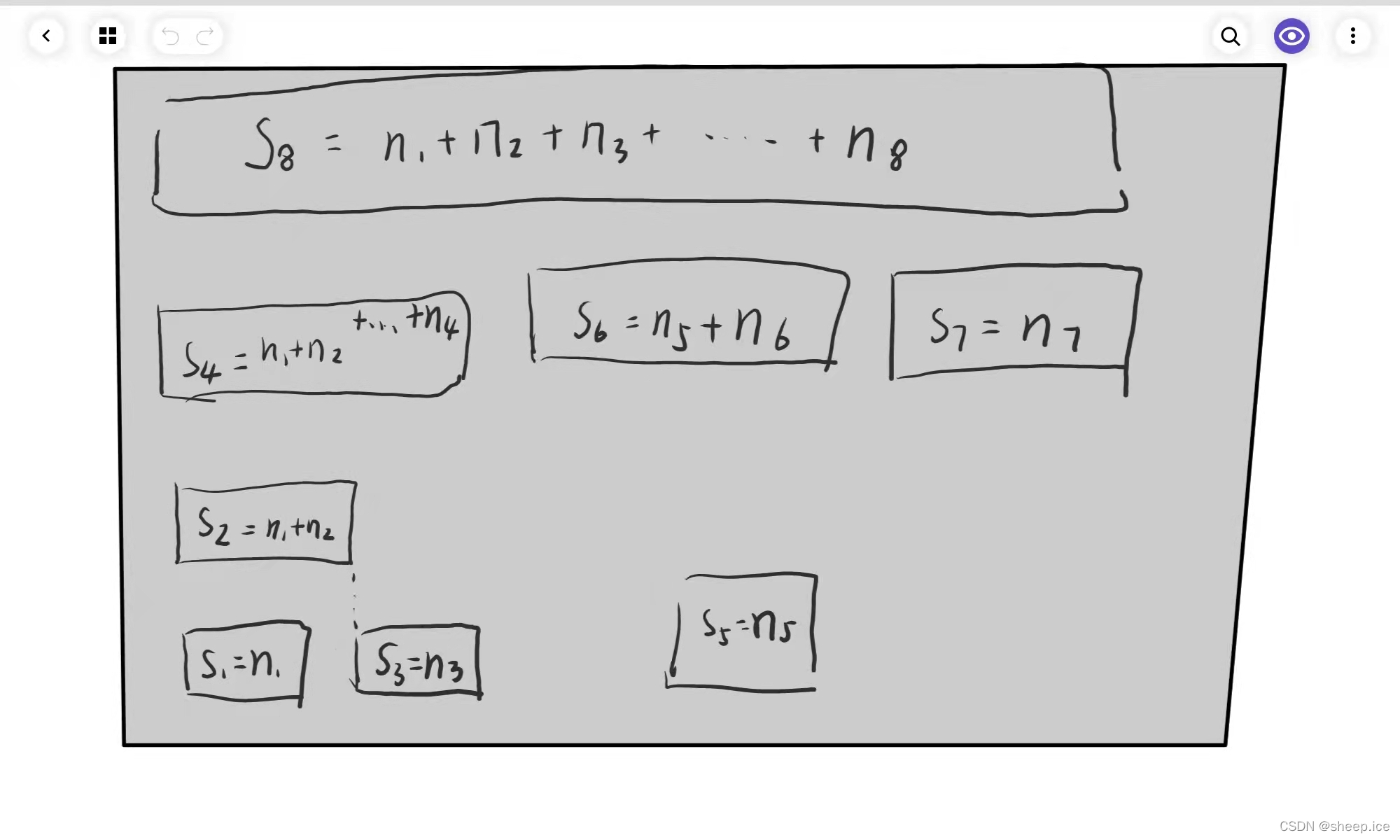
大家可以看到,树状数组首先对应一个s数组(假设有8个元素),也就是一个求总和的数组,这个数组里面对应装下一些前缀和,而每一个s对应数都是连续的,这也就为我们后面提供区间和利用前缀和的思想提供了很好的办法!
==当然这里有要注意的点:== 就是我们的s数组必须从1作为下标开始,也就是8个元素我们要开s[9]的空间,因为lowbit(0)是不存在最低位1的会造成无限循环的风险。大家可能不太理解,这个数组里面为什么能够按照这样的数字进行相加,我们看下面的图: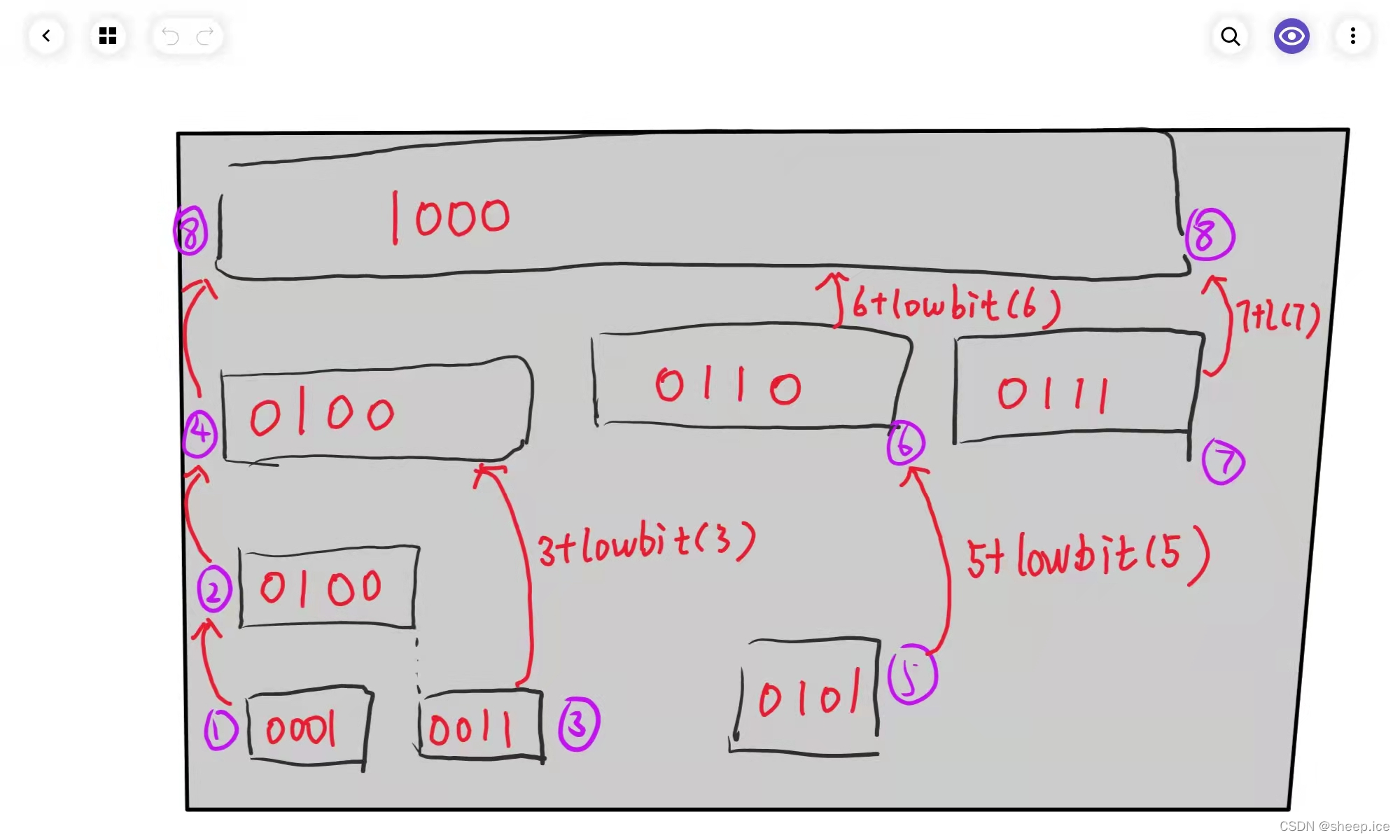
从上面的图,我们可以知道,每个s对应的下标,都是从某个下标i,通过加上lowbit(i),并且在每次演变的时候,让$S_i$加上对应的num[i - 1] 的数(因为num数中的下标是从0开始的),最后就变成了第一张图的样子,也就是接下来要讲的区间的更新。
四、区间的查询以及更新
①区间的更新:
因为有了上面的铺垫,我们直接放上,s数组更新的一个代码,也就是如何让s数组存上对应相关的值。
//添加和到对应的树状数组
void add(int x, int val) {
for(int i = x; i <= n; i += lowbit(i)) {
sum[i] += val; //这里的val其实就是num[i - 1];
}
}经过上面的操作之后,我们就完成了s数组的构建,那么如果题目要求,改掉num数组里面的某个数的话,我们只需要让那个数所在的s也同时的更新就好,像下面一样:
void update(int index, int val) {
//这里的index要+1,因为num数组的下标从0开始
add(index + 1, val - nums[index]);
nums[index] = val;
}②区间的查询
区间的查询,其实有点像更新的逆过程,比如我们要知道$\sum_{i=0}^{6}num[i]$的总和也就是说如何要求出$ S_7 + S_6 + S_4 $的值(这里大家可以对照一下上面的图)。7 - 6 - 4 不就是 111 - 110 - 100的过程吗?那其实就是每次让下标为i的数减去lowbit(i),然后在此过程中去加上S[i]的值,最后就可以得到原始下标为index的前缀和了,根据区间前缀和计算的方式,最终就可以知道一段区间的和了。
//计算从下标0- x-1的前缀和
int query(int x) {
int s = 0;
for(int i = x; i > 0; i -= lowbit(i)) {
s += sum[i];
}
return s;
}
//计算区间的和(不了解前缀和的同学可以先了解一下前缀和)
int sumRange(int left, int right) {
//因为原始的下标从0开始,那么对应区间和的下标要加1
return query(right + 1) - query(left);
}五、力扣的原题
①原题贴图
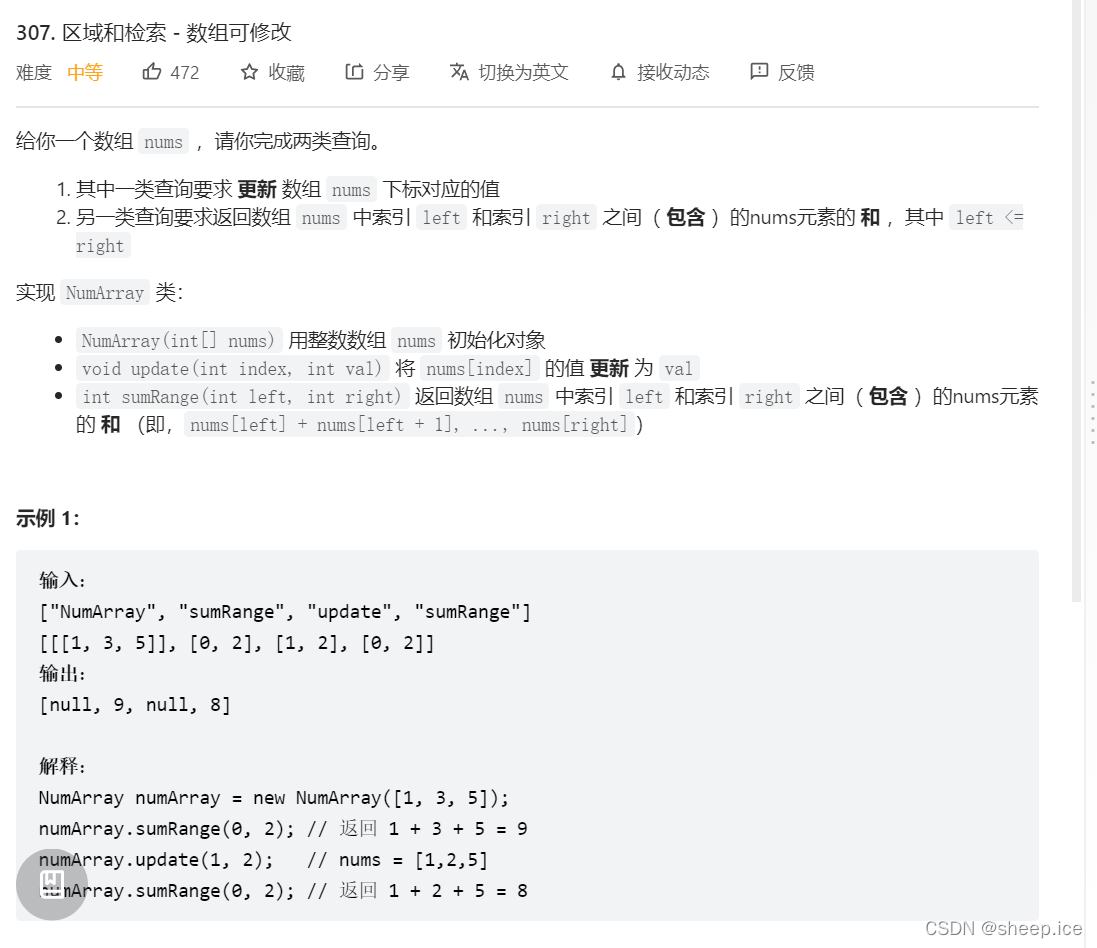
②AC的代码全贴
class NumArray {
public:
vector<int> sum;
//记录最低位的1
int lowbit(int x) {
return x & -x;
}
//添加和到对应的树状数组
void add(int x, int val) {
for(int i = x; i <= n; i += lowbit(i)) {
sum[i] += val;
}
}
int query(int x) {
int s = 0;
for(int i = x; i > 0; i -= lowbit(i)) {
s += sum[i];
}
return s;
}
vector<int> nums;
int n;
NumArray(vector<int>& nums) {
this->nums = nums;
n = nums.size();
sum.resize(n + 1, 0);
for(int i = 0; i < n; i++) {
add(i + 1, nums[i]);
}
}
void update(int index, int val) {
add(index + 1, val - nums[index]);
nums[index] = val;
}
int sumRange(int left, int right) {
return query(right + 1) - query(left);
}
};


